金属結晶(体心立方格子・面心立方格子・六方最密構造・原子半径・充填率など)

---

金属結晶と結晶格子

多くの金属結晶の結晶格子が「体心立方格子」「面心立方格子」「六方最密構造」に分類されます。
以下の表は、これらの特徴をまとめたものです。(後に説明する内容を含みます。)

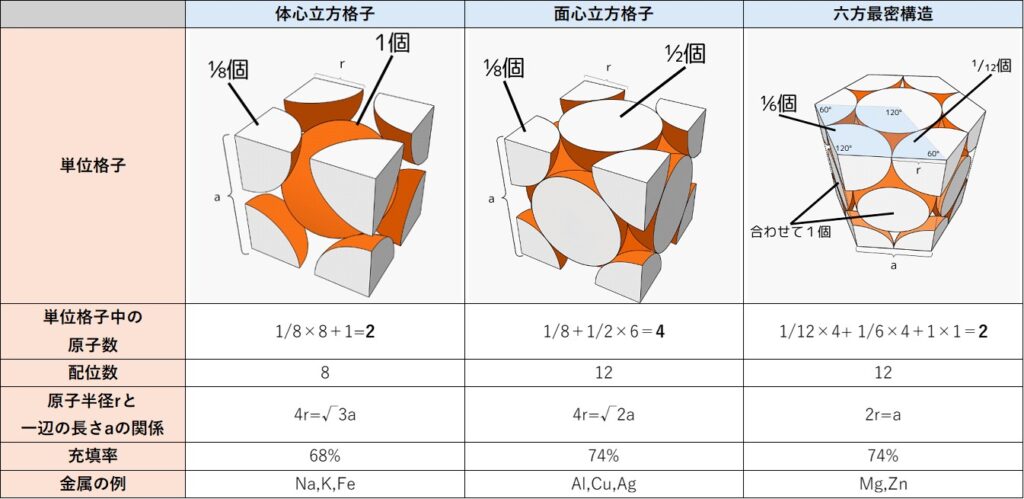
まず、各結晶格子の概要・原子の数・配位数について見ていきましょう。

---

体心立方格子

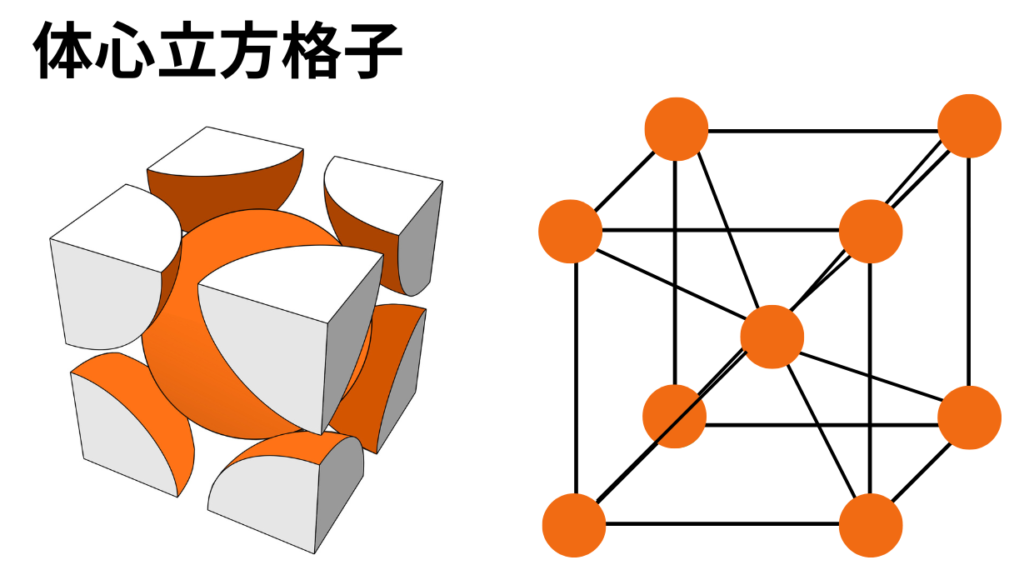
【概要】
上図のように、立方体の各頂点と立方体の中心に金属原子が配列された結晶格子を体心立方格子といいます。

【原子の数】
各頂点の原子が\(\frac{1}{8}\)個分、真ん中の原子が1個分なので体心立方格子の原子の数は2個になります。

【配位数】
真ん中の原子に着目すると、各頂点に8個原子があるため配位数は８になります。

---

面心立方格子

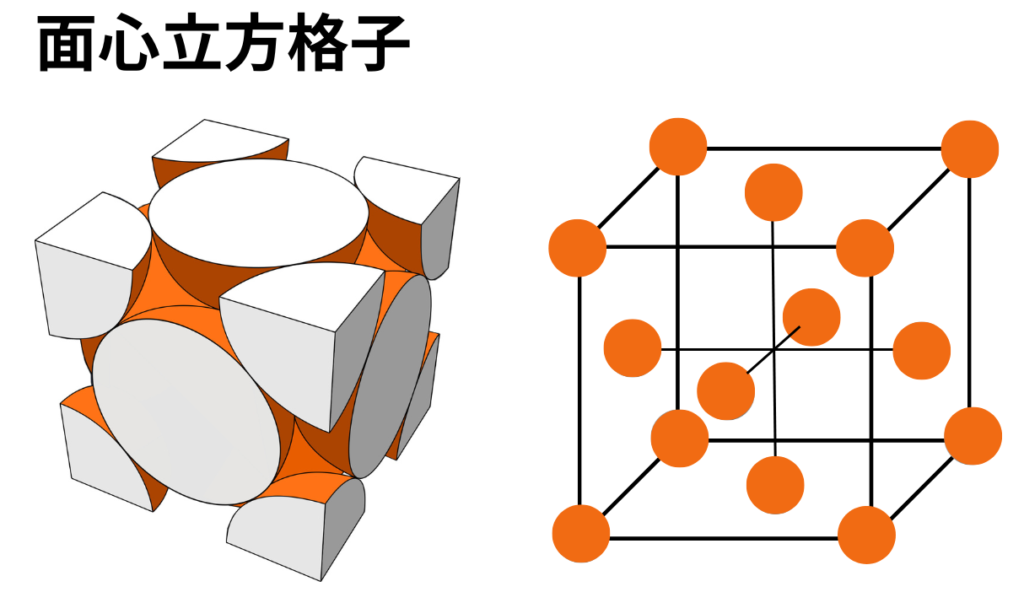
【概要】
上図のように、立方体の各頂点と各面の中心に金属原子が配列された結晶格子を面心立方格子といいます。

【原子の数】
各頂点の原子が\(\frac{1}{8}\)個分、各面の中心の原子が\(\frac{1}{2}\)個分なので面心立方格子の原子の数は4個になります。

【配位数】
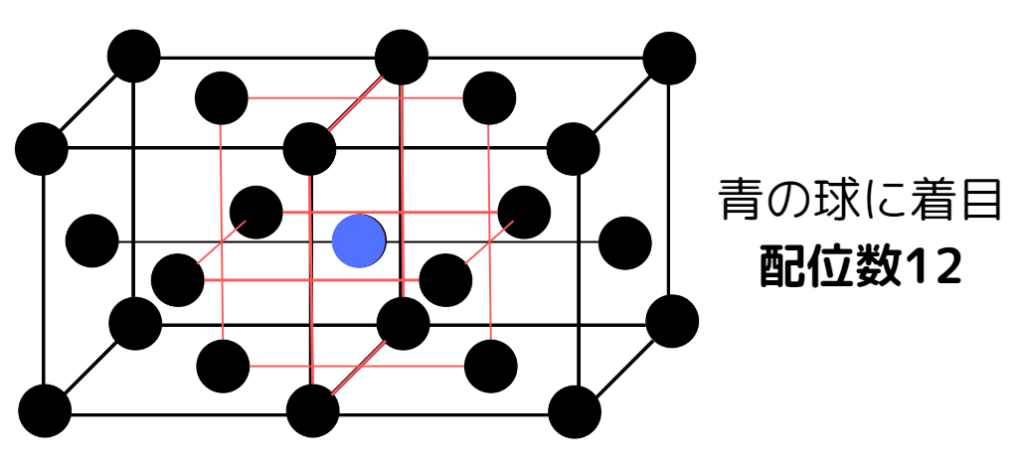
下図のように横に面心立方格子を2つ並べてみると、配位数が12であることがわかります。

---

六方最密構造

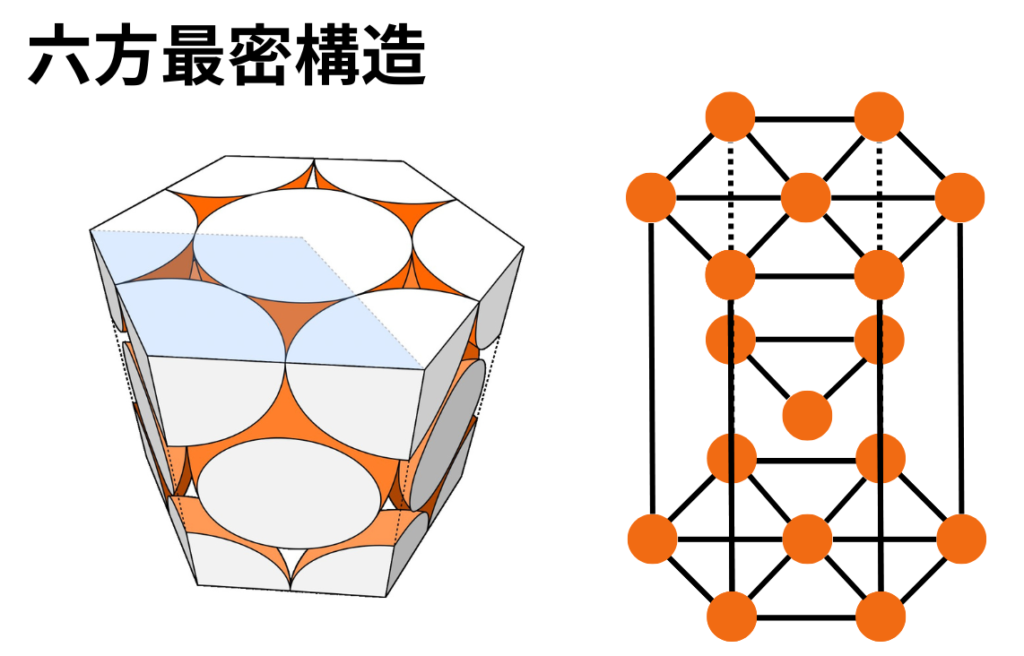
【概要】
上図のように３つの原子の層と７つの原子の層をくり返し配列させた結晶格子を六方最密構造といいます。

【原子の数】
六方最密構造の単位格子は図の青い部分(構造を三分の一に切り分けた部分)になります。頂点にある中心角60°の原子4個が\(\frac{1}{12}\)個分、頂点にある中心角120°の原子4個が\(\frac{1}{6}\)個分、二層目の原子が2つ合わせて1個分なので六方最密構造の原子の数は2個になります。

【配位数】
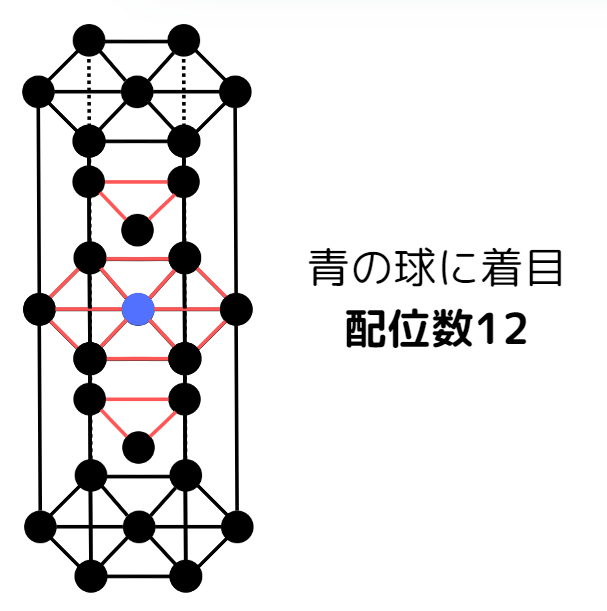
下図のように縦に六方最密構造を２つ並べてみると、配位数が12であることがわかります。

---

原子半径

結晶格子の一辺の長さが分かっていると、構成する金属原子の原子半径を求めることが出来ます。
体心立方格子と面心立方格子の原子半径を求めていきましょう。

---

体心立方格子の原子半径

体心立方格子の一辺の長さをa、構成する原子の原子半径をrとします。
体心立方格子の場合、立方体の対角線上で各原子が接しているため下図のように斜めに切って平面を取り出します。

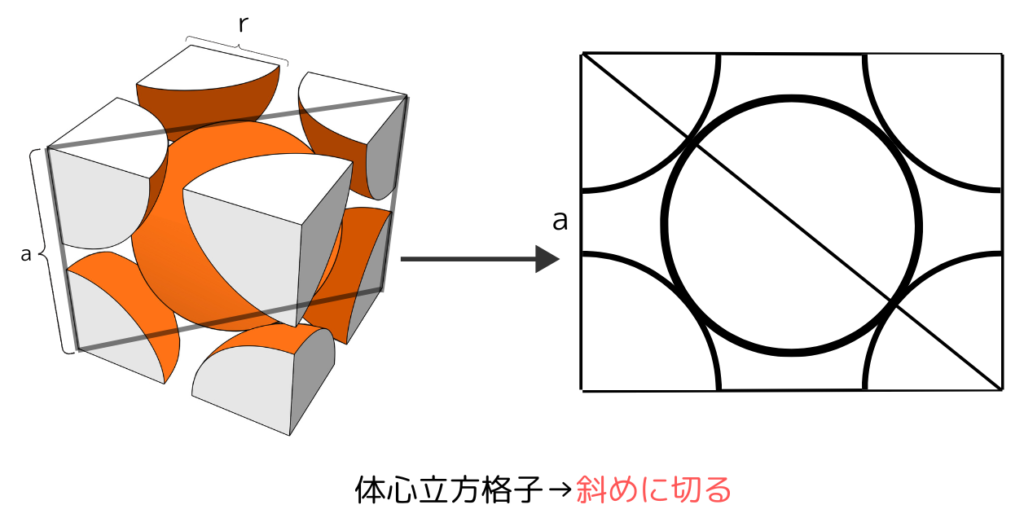
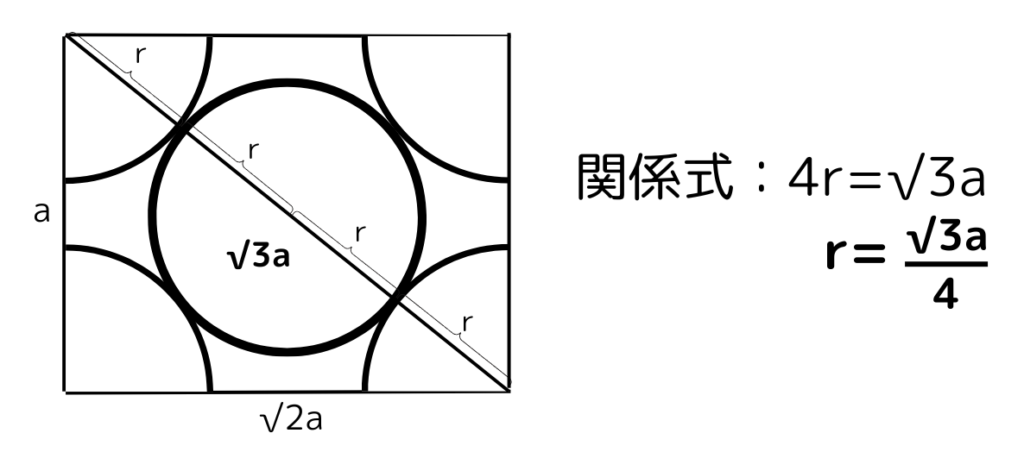
切った断面は縦の長さa、横の長さ√2a(立方体の面の対角線の長さ)、対角線の長さ√3a(三平方の定理より)の長方形になります。

また、対角線の長さは半径r×４とも見れるため√3a＝4rの関係式が成り立ち、rを求める事ができます。

---

面心立方格子の原子半径

面心立方格子の一辺の長さをa、構成する原子の原子半径をrとします。
面心立方格子の場合、各面の対角線上で各原子が接しているため下図のように1つの面を取り出します。

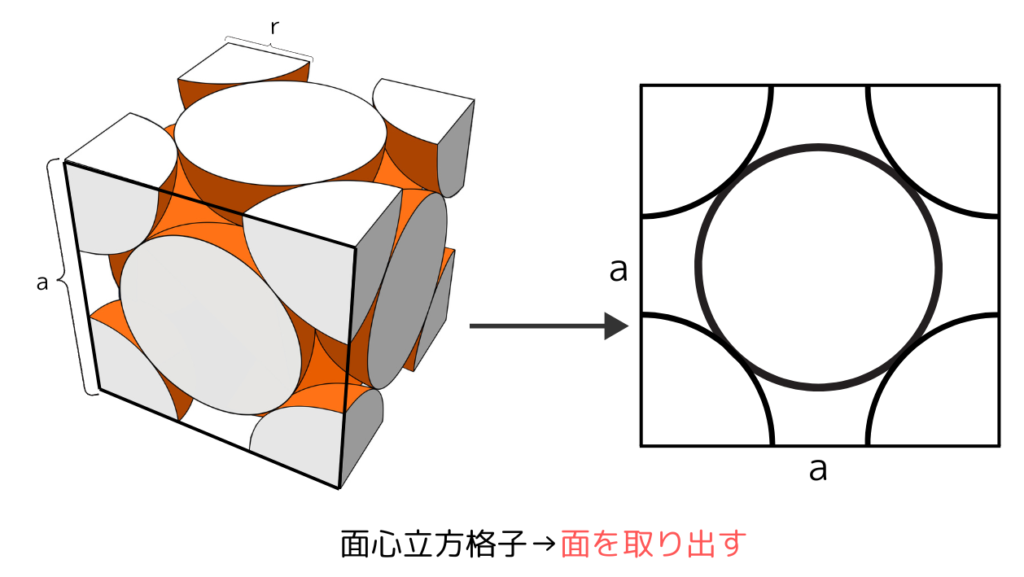
面は縦・横の長さa、対角線の長さ√2aの正方形になります。

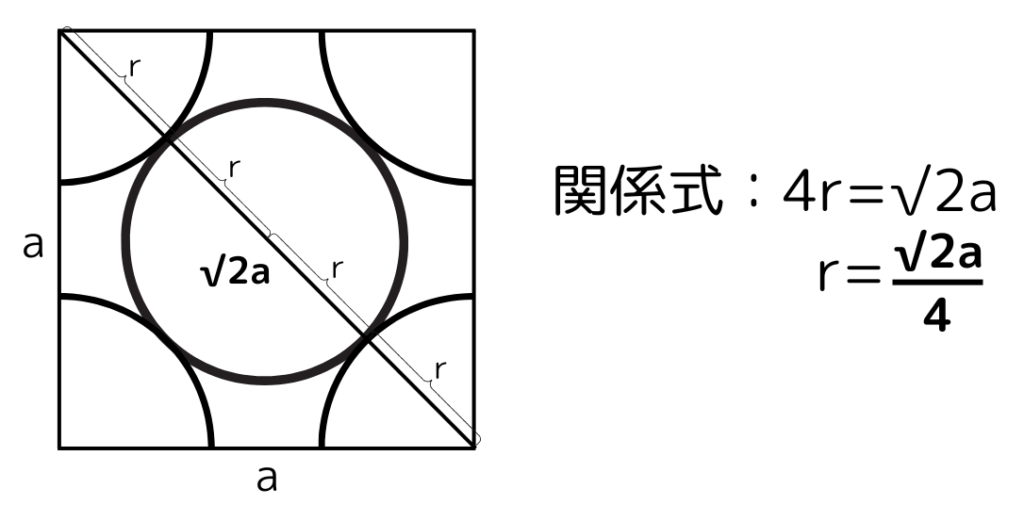
先ほどと同様に、対角線の長さは半径r×４とも見れるため√2a＝4rの関係式が成り立ち、rを求める事ができます。

---

充填率

「単位格子の体積のうち原子がどのくらいの体積を占めているか」を示した割合を充填率といいます。
充填率は次のように求めることができます。

充填率＝\(\frac{単位格子中の原子の体積}{単位格子の体積}\)

先ほど「原子半径r」を「単位格子の長さa」で表したので、「単位格子中の原子の体積」と「単位格子の体積」もaで表すことができ、充填率を求めることができます。

ここからそれぞれの結晶格子の充填率を求めていきましょう。

---

体心立方格子の充填率

「単位格子中の原子の体積＝単位格子中の原子の数×原子１つの体積(球の体積)]の関係と先ほど求めたr=\(\frac{√3a}{4}\)を使うと、

体心立方格子の充填率＝\(\frac{2×\frac{4πr³}{3}}{a³}\)=\(\frac{2×\frac{4π×\frac{3√3a³}{64}}{3}}{a³}\)=\(\frac{√3π}{8}\)≒0.68

以上より、体心立方格子の充填率は0.68(68%)になります。

---

面心立方格子の充填率

体心立方格子と同様に、r=\(\frac{√2a}{4}\)を使うと、

面心立方格子の充填率＝\(\frac{4×\frac{4πr³}{3}}{a³}\)=\(\frac{4×\frac{4π×\frac{2√2a³}{64}}{3}}{a³}\)=\(\frac{√2π}{6}\)≒0.74

以上より、面心立方格子の充填率は0.74(74%)になります。

---